草津七福神めぐり〜遺伝的アルゴリズム編〜

新年早々引いたおみくじが「末吉」という冴えない結果だったので、何とかして今年の福を招かなくては…と思っていたら、縁起の良さそうなイベントの告知が目に留まりました！

『草津七福神めぐり』

草津宿界隈の七福神にゆかりのある神社や寺社を巡って、スタンプを集めるという歴史散策好き垂涎のイベントです。

目的地は下記の通り。

0. くさつ夢本陣（スタート＆ゴール）
1. 養専寺（布袋尊）
2. 真願寺（寿老人）
3. 立木神社（弁財天）
4. 道灌蔵（大黒天）
5. 小汐井神社（恵美須天）
6. 伊砂砂神社（福禄寿）
7. 神宮寺（毘沙門天）

真願寺や神宮寺など初めて聞くマニアックな場所もあるので、まずは目的地を地図にプロットしてみました。

おおむね旧東海道・旧中山道沿いに並んでいますが、よく見ると寺はメインの通りから外れた裏路地に建っており*1、ただ単に旧街道を真っすぐ行けば全部巡れるというわけではなさそうです。

では、どのようなルートで七福神を巡るのが最も効率的でしょうか。

出発地である「くさつ夢本陣」でスタンプラリーの台紙をもらい、七福神を祀るスタンプポイントすべてを一度ずつ訪問した後、再び出発地の「くさつ夢本陣」に戻ってきて粗品をもらう。

このときの総移動距離が最短の経路を求める問題…

これってもしかして…

「巡回セールスマン問題」（Traveling Salesman Problem）！！？

巡回セールスマン問題
セールスマンが $n$ 個の都市すべてを一度ずつ訪問して出発地に戻ってくるときの移動距離が最小になるような経路を求める組み合わせ最適化問題

いや、ここは「巡回七福神問題」とでも呼ぶべきでしょうか。
ちょうど略称も本家と同じ「TSP」ですし。

では、解いてみましょう。

今回の「巡回七福神問題」は次のようなグラフで表現できます。

f:id:fffw2:20180120102901p:plain

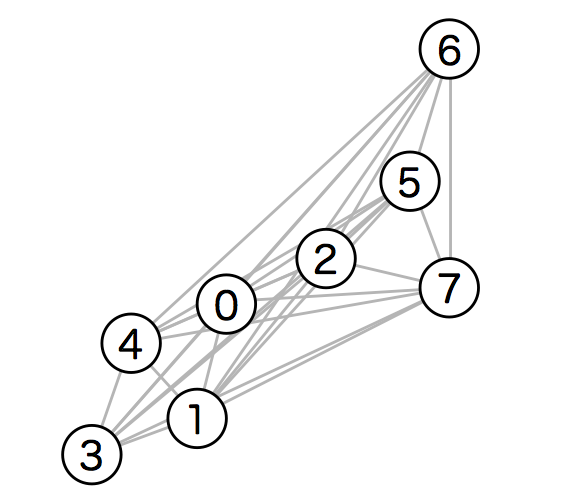
丸囲みの番号は「訪問場所」、灰色の線は「道」を単純化したものです。グラフ理論で言うところの「ノード（節点）」と「エッジ（辺）」です。

0 がスタート地点のくさつ夢本陣です。ここを出発して、 1〜7 の七福神を訪問したのち、再び 0 に戻ってきます。

2 点間の道のりは GoogleMap で経路検索して調べられます。例えば、1：養専寺と 3：立木神社の道のりを調べると、270m です。これを $d_{1,3} = 270$ と表現することにします。*2

（…10分後…）

すべての道のりを調べ終わりました。

$d_{0,1} = 400, d_{0,2} = 220, d_{0,3} = 500, \ldots$
と書き下していくと非常にわかりづらいので、行列で書きます。

f:id:fffw2:20180121213143p:plain

$i$ 行 $j$ 列の成分が、訪問場所 $i$ から訪問場所 $j$ への道のりを表しています。

これで準備は整いました！

経路の組み合わせを考えていきましょう。

(i) 0→1→2→3→4→5→6→7→0 というルートを選ぶ場合
　 $d_{0,1}+d_{1,2}+d_{2,3}+d_{3,4}+d_{4,5}+d_{5,6}+d_{6,7}+d_{7,0}\\\ = 400+450+700+280+850+700+1400 \\\ =4780$
道のりは4780m

(ii) 0→1→2→3→4→5→7→6→0 というルートを選ぶ場合
　 $d_{0,1}+d_{1,2}+d_{2,3}+d_{3,4}+d_{4,5}+d_{5,7}+d_{7,6}+d_{6,0}\\\ = 400+450+700+280+650+1400+1300 \\\ =5180$
道のりは5180m

…って、これ何回やらなきゃダメなんです？？？

すべての経路の中から総当たりで最短経路を求めようとすると、
訪問場所が $n$ 個のとき、 $\displaystyle \frac{(n-1)!}{2}$ 通りの経路を考えなくてはなりません。*3

訪問場所が20個でも、
経路は全部で60,822,550,204,416,000通りです。約6京。
1秒間に1億通りの経路を計算できるコンピューターを用いても、約19年掛かります。
階乗の力、恐るべし。

七福神問題では、スタート地点も含めてたった8箇所をめぐるだけなので、
$\displaystyle \frac{(8-1)!}{2}=2520$ 通りの経路を考えるだけでよく、これぐらいならコンピューターの力を使えば総当たりでも解けてしまうのですが、いつか西国三十三所をめぐることもあるかもしれないので、訪問場所が多い場合にも使える一般的な解法を考えておきたいと思います。

総当たりで厳密な最短経路を求めるのは、現実的な時間では不可能ですが、必ずしも厳密とは言えないが最短経路にある程度近い解 であれば、いくつかのアルゴリズムで導出できることが知られています。*4

今回は、数あるアルゴリズムの中でも、私のお気に入りの「遺伝的アルゴリズム」を使って解いてみようと思います！使いこなせる自信があるのが「遺伝的アルゴリズム」ぐらいだからです。

遺伝的アルゴリズム

「遺伝的アルゴリズム」は、1975年にミシガン大学のホランド先生が考案したアルゴリズム *5です。生物の進化の手法を情報学に組み込むという非常に面白いアルゴリズムです。

私は大学2回生のときに授業で「遺伝的アルゴリズム」を習い、「なんだこの斬新なアルゴリズムは！！！！？」と衝撃を受けました。

適用範囲は幅広く、電子回路設計、物資配送計画、新幹線N700系のフォルムの最適化、スーパーマリオブラザーズの1-1のクリア、ピカチュウの歩行学習など、多種多様な問題に対して適用されています。

大雑把に言うと、次のような流れのアルゴリズムです。

ランダムに個体群を用意します。
二人ずつのペアを作り、親の遺伝子を受け継いだ子供を生み出します。
強い子供たちが生き残り、弱い子供たちは死にます。
強い子供たちが次世代の親になります。
2〜4を繰り返すと最強の個体ができあがります。

「ふーん、よくある生物の話だよね。これでどうやって問題を解くの？」
…と思うことでしょう。私も思いました。

なんと解きたい問題を遺伝子に乗せるのです！

調べたい組み合わせの候補を「遺伝子」で表現し、その遺伝子配列を評価し、最適解に近いほど「強い」個体であると考えます。すると、交雑・淘汰を繰り返したら…
自然と最適解（に近い解）が生き残るのです！生命の神秘！！

実際に遺伝的アルゴリズムを使ってみましょう。

1. ランダムに個体群を用意します。

七福神 1〜7 をめぐる順番を遺伝子配列で表した個体群を用意します。

Aさんの遺伝子配列：7143526
Bさんの遺伝子配列：4175623
Cさんの遺伝子配列：5762413
Dさんの遺伝子配列：7346215

スタートとゴールは 0 で固定なので、省略しました。

それぞれの経路で歩くときの経路長を $d_{i,j}$ を用いて計算すると、次のようになります。（スタート(0)→最初の七福神、最後の七福神→ゴール(0) の道のりも含む点に注意）

Aさんの遺伝子配列：7143526（6330m）
Bさんの遺伝子配列：4175623（5100m）
Cさんの遺伝子配列：5762413（5320m）
Dさんの遺伝子配列：7346215（6930m）

この中で経路長が最短なのはBさんなので、Bさんが一番「強い」個体であるということになります。

2. 二人ずつのペアを作り、親の遺伝子を受け継いだ子供を生み出します。

ペアを作って子供を作ります。遺伝的アルゴリズムでは性別は考えません。子供の遺伝子配列は、次の2通りで生成します。

片方の親の遺伝子配列をそのままコピーした遺伝子配列にする（完全連鎖）
両親の遺伝子配列の一部を交換した遺伝子配列にする（交叉）

交叉（乗換え）は、相同染色体間で起こる遺伝子の部分交換です。高校で生物を履修していた人なら聞き覚えがある用語だと思います。これによって遺伝的多様性が生じます。遺伝的アルゴリズムを使うだけなら、生物学における交叉の概念がよくわからなくても大丈夫ですので、ここではイメージ画像だけ貼って詳しい説明は省略します。

f:id:fffw2:20180120225529p:plain
（『サイエンスビュー生物総合資料』実教出版、p.64 より引用）

例えば、AさんとBさんの子供は次のようなパターンになります。

Aさん：7143526
　×
Bさん：4175623
　↓
子供α：7143526（Aさんの遺伝子配列のコピー）
子供β：7145623（交叉した遺伝子配列）
子供γ：4173526（交叉した遺伝子配列）
子供δ：4175623（Bさんの遺伝子配列のコピー）

ただし、今回の問題の場合、「7つの場所すべてを一度ずつ訪問しなくてはならない」という縛りがあるので、交叉によって生成された遺伝子配列に同じ数字（遺伝子）が含まれていてはいけません。遺伝子重複によって死に至ります。

Cさん：5762413
　×
Dさん：7346215
　↓
子供ε：5762413
子供ζ：5762215（致死個体：2, 5が重複）
子供η：7346413（致死個体：3, 4が重複）
子供θ：7346215

遺伝子重複による致死個体が生じないような交叉のやり方として、「順序交叉」*6という方法が考案されているので、これを使ってみましょう。

Dさんの遺伝子配列に着目して、
切断点の左側にある遺伝子を切断点の右側に持ってきます。
Cさん：5762｜413
　×
Dさん：7346｜215
　↓
Cさん：5762｜413
　×
Dさん：｜2157346
Cさんの切断点の左側にある「5762」と重複している数字を
Dさんの切断点の右側にある「2157346」から削除します。
Cさん：5762｜413
　×
Dさん：｜2157346
　↓
Cさん：5762｜413
　×
Dさん：｜134
遺伝子重複のない元気な子供が生まれます。
子供ζ'：5762｜134　＜ｵｷﾞｬｰ

この方法なら確実に遺伝子重複が発生しないので、命を無駄に失わず、多様な遺伝子配列をもった子供をどんどん作ることができます！

3. 強い子供たちが生き残り、弱い子供たちは死にます。

2.の操作の結果、バラエティー豊かな子供たちが生まれて賑やかになります。

子供α：7143526
子供β：7145623
子供γ：4173526
子供δ：4175623

子供ε：5762413
子供ζ'：5762134
子供η'：7346152
子供θ：7346215

しかし、可愛そうですが、この世に生き残れる個体数は限られています。環境への適応度が高い個体のみが生き残り、適応できなかった個体は死にます。これが自然の摂理なのです。

今回の問題では「経路長」が短い子供だけが生き残ります。
生き残れる個体数を 4 とすると…

子供δ：4175623（5100m）
子供ζ'：5762134（5150m）
子供ε：5762413（5320m）
子供β：7145623（5800m）
─ 以下の子供たちは死亡 ─
子供α：7143526（6330m）
子供γ：4173526（6750m）
子供θ：7346215（6930m）
子供η'：7346152（7000m）

子供 δ、ζ'、ε、β の4名が生存します。

このように適応度が高い「強い」個体だけが生き残るように弱者を淘汰していく方法を、遺伝的アルゴリズムの言葉で「エリート選択」といいます。

4. 強い子供たちが次世代の親になります。

3. の操作によって生き残った子供たちは、成長して次世代の親になります。次世代の親集団は優秀で、最初の親集団より平均経路長が短くなっています。

第1世代（A, B, C, D）の平均経路長は 5920m
第2世代（δ, ζ', ε, β）の平均経路長は 5342.5m

5. 2〜4を繰り返すと最強の個体ができあがります。

2〜4の交雑・選択操作を繰り返していき、第3世代、第4世代、第5世代、…と世代を重ねていくと、エリート選択の力でどんどん個体群は優秀になっていきます。そして、最終的に最強の個体（＝最短経路）が誕生して進化が収束します！

ここまでの一連の流れを手作業で行うのは流石に無謀なので、コンピューターにお願いしてやってもらいます。やっつけで150行ぐらいのプログラムを書きました。おりゃっ。

f:id:fffw2:20180121014037p:plain

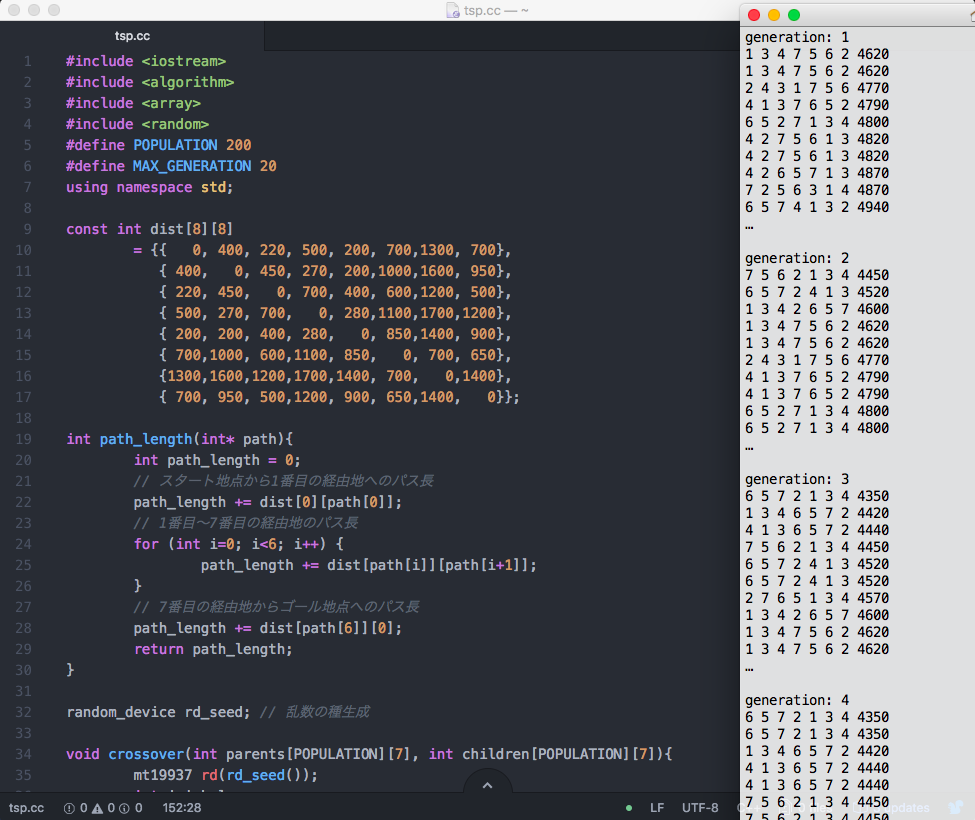
交叉の実装がちょっと面倒でした… _(:3 」∠)_

個体数を 200 に設定してプログラムを動かしてみたところ、問題の規模が小さいため、あっという間に進化は収束。

f:id:fffw2:20180121044120p:plain
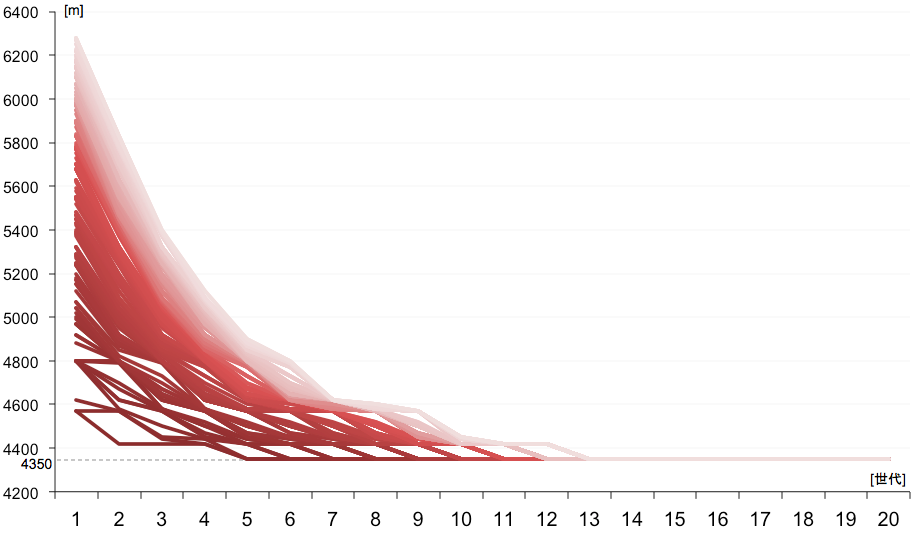
各世代の上位200個体の経路長の推移を表したグラフ
（縦軸は各個体の経路長、横軸は世代）

進化の結果、導かれた最短経路は…

6→5→7→2→1→3→4（4350m）でした！！（逆回りも可）

f:id:fffw2:20180121045818p:plain

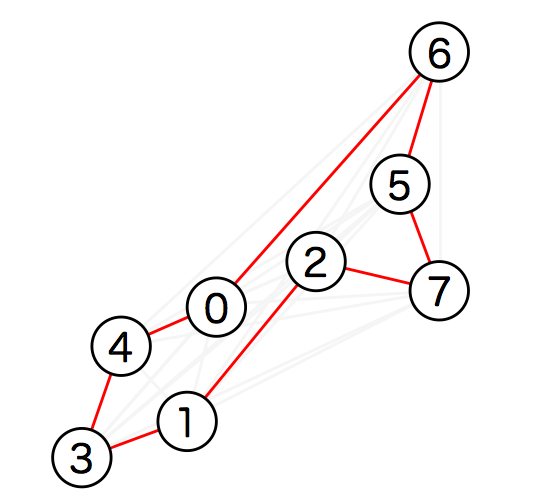
GoogleMapに経路を描いてみると、こうなります！
じゃーん！

こうして、無事に「巡回七福神問題」を解いた私は、最短経路を描いた地図を片手に、無駄のない動きで草津の七福神をめぐり、平成30年の福を祈ることができたのでした。めでたしめでたし。

f:id:fffw2:20180121052547j:plain

立木神社で、七福神めぐりをしている親子から声をかけられました。お母さん曰く「息子が地図を見ながらルートを考えたのよ」とのこと。息子さんの手には、小学生らしく自由闊達に描かれた地図が握られていました。地図とにらめっこしながら一生懸命ルートを考えたんだろうなあ。微笑ましい。

「お兄さんはコンピューターを使って最短経路を導いたよ！(｀･ω･´)
　少年よ、4350mでめぐれる正解ルートを教えてあげようか？」

と言いたくなりましたが、そんな無粋な真似は悪いので、ぐっと堪えて「えらいねー」と言っておきました。

その後、不思議なことに、養専寺、真願寺、神宮寺、…と私の行く先々で同じ親子がいるではありませんか。どうやら最初から最後まで私と全く同じルートでめぐっていたようです。むむむ。

少年は一体どんなアルゴリズムで「巡回七福神問題」を解いたのでしょうか。

*1:寺院が裏路地に建っているのは、江戸時代、寺院の土地が「除地」と呼ばれる非課税の土地だったため。主要街道沿いは間口税を課せるので、課税対象である町屋が置かれました。

*2:「d」は「distance」の頭文字

*3:スタート地点とゴール地点が同じなので訪問経路の場合の数は「円順列」と同じ考え方になります。さらに、経路を逆回りしてもOKなので、2で割ります。これは「数珠順列」と同じ考え方です。

*4:こういった解法を「ヒューリスティックな」解法と言います。焼きなまし法、山登り法、タブー探索、遺伝的アルゴリズム、アントコロニー最適化、などがあります。試行錯誤を繰り返して正解に近づいていく解法です。「heuristic」とは「発見的な」という意味で、古代ギリシャ語由来の言葉です。入浴中に浮力の原理を発見したアルキメデスが「heureka! heureka!」（見つけた！見つけた！）と叫びながら街中を全裸で走り回ったという逸話はあまりにも有名ですね。

*5:J. H. Holland, Adaption in natural artificial systems, 1975.

*6:L. Davis, Applying Adaptive Algorithms to Epistatic Domains, 1985.

ふれっしゅのーと

趣味に生きる30代エンジニアが心に移りゆくよしなし事をそこはかとなく書きつくるブログ